そろばんのレベルや合格点～3級～

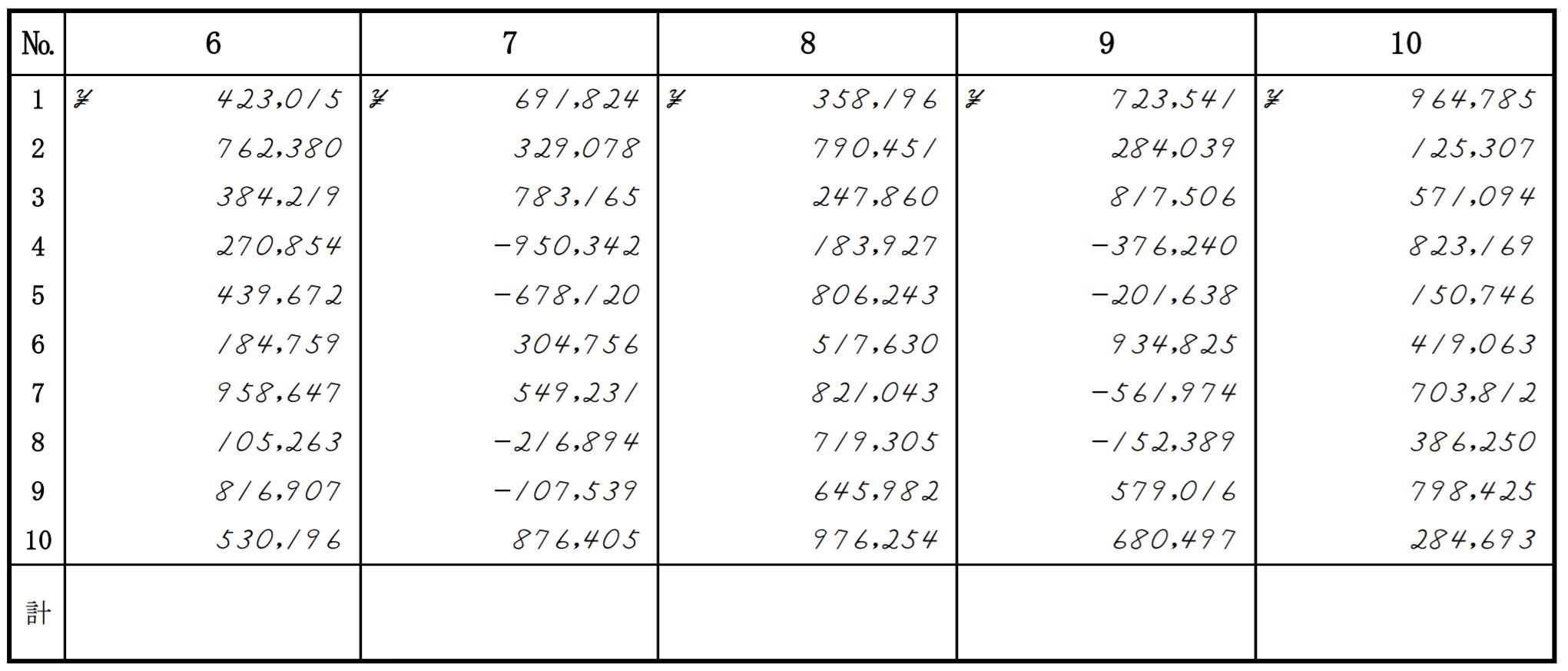
以前にも説明した通り、ピコ検定では4級までの難易度がかなり上がっていますが、3級からは日商検定に（レベルが）揃います。これにより、3級の合格率を飛躍的に上げているのですが、その代表は見取り算ですね。
5桁～3桁変動15口（4級）→6桁固定10口（3級）なのでレベルは殆ど変わらないどころか、桁が固定されている分、やりやすい場合もあるかもしれません。珠をはじく回数は殆ど同じと言っても良いくらいでしょう。
後述しますが、いつもなら点数を取りやすい割り算で“割り切れない”問題が出てくるので、見取りでしっかりと点を取っていきたいところです。

6桁10口という事は1問につき60回10問で約600回。制限時間は600秒なので、1秒で1つの数字をクリアすれば大体クリアできます。ですので、焦らず確実にいきましょう。4級をクリアした今、割と余裕に行けるはずです。

あるとすれば１度に長い引き算がやってくるので、ここは気を付けたいところです。
さすがに迷っている暇はありませんよ^^;

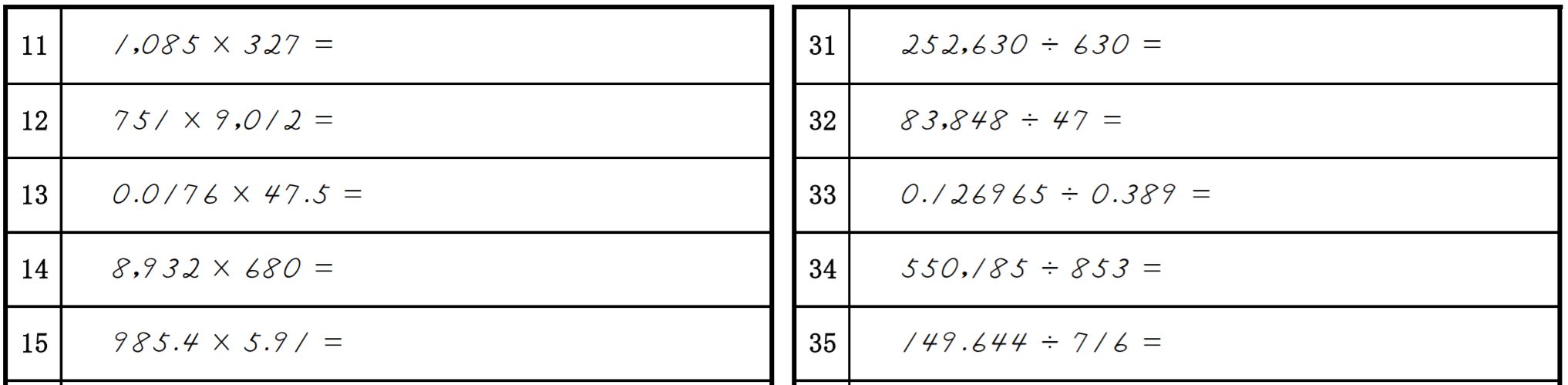
準3級以上で出題される少数の計算と言うのは必要以上に問題が難しく見えます。
何故なら、計算する数字以外に0.0など余計な数字が入ってきて、桁数が多く見えるから。なので、苦手意識を持たせないことが重要。よって、まずはかけ算わり算を解説する前にこちらを説明しておきます。

たとえば、 2.5×0.0371とあると、やたらに桁数が多く、計算する前に尻込みしてしまうことが考えられますが、ここで計算すべきなのは25×371です。
あとは少数点がどこにつくのか、四捨五入は必要なのか、確認すれば良いだけです。
そんな難しくないことはお分かりいただけたと思います。

ここでいう位取り＝少数点をどこにつけるか、と思っていただいて結構です。
方法は大きく分けて２種類。

【１】 初めから小数点を決めて計算。そのまま記入する
【２】 小数点を完全無視して計算。問題から桁数を導き出す。

ピコではどんな学年でもわかりやすく指導できるように【１】の方法を採用しています。
初めはミスが少なく、わかりやすい【１】の方法で行い、完全にマスターして更に時間短縮したい場合は【２】の方法へ移行すると良いのでは無いでしょうか。
両方のやり方を選択して使用することも（慣れれば）比較的容易です。
※3級の間にやらなくてはいけない事ではなくて、3級 2級 1級と進んでいく上で徐々に変化していけば良いです

まずはピコ式の【１】から説明していきます。
例題：69.458×4.5
数字は下記画像の様に入れます。小数点以下の458は定位点より右側に置きます。

そして45を入れる場所は適当で大丈夫です。ここに拘ってはいけません。
片落としの場合は置かないで計算できますね。
そして位取りです。
着目すべきは4.5。（かける数、そろばんでは法（ほう）といいます）
この数字は1桁。1桁に1桁加えて2桁。※
“定位点から2つ右にずれた場所”が1の位になります。ここに左手の人差し指を置いて計算、終了した時点では下記画像の様になります。

よって答えは312.561となります。とても簡単でしょう。
このやり方の良い部分は左手を置いた後は“計算に集中できる”という事です。

※例えば法が3桁の場合は4つ右にずれます。

この考え方を使用して、0.いくつ（右に一つ）や0.0いくつ（定位点から動かない）の問題も対応することが容易になります。

続いて【２】を説明します。
例題：69.458×4.5
少数点を除いた部分に着目します。2桁×1桁ですね。そして単純に足し算をします。
答えは3桁と推測できますね。
そしたら計算開始です。置く場所は極論すると、どこでも大丈夫です。

（どこに置いても大丈夫）

計算すると3125610と計算できますので、3桁目と4桁目の間に小数点を入れます。つまり312.561。

非常に簡単ですね。この方法を使うときのメリットは置く場所を適当に決められることです。後から位取りをするので、全て同じ場所から数字を入れ始めたり、など、小数点に縛られることなく、自分の思い通りに操ることが出来ます。

ですが、69.458×1.1の場合はどうでしょう。この場合、3桁ではなく、2桁になってしまい、間違いに気を付けなくてはいけません。
こういった事も理解し、気を配って更に時間短縮できる場合は【２】の方法を試してみる価値があります。（個人的に言ってしまうと、小学生のうちはあまりお勧めできません）

3級の桁数自体は4×3桁が基本、そこだけ見れば4級と同じです。
つまり、レベルとしてはほぼ変わらないので、位取りをしっかり定着させ、集中して計算出来れば合格への道のりはそう遠くありません。
要点をおさえ、苦手意識を遠ざけてしっかりと点を積み重ねましょう。

さて、続いてわり算を進めます。
かけ算が出来ればわり算の位取りは簡単。やはり大まかに方法は２種類。

【１】初めから小数点を決めて計算。
【２】小数点を完全無視して計算。問題から桁数を導き出す

【１】の場合、法の桁数に1をたして右にずれましたが、わり算の場合は法の桁数に1をたして”左に”ずれます。これだけです^^;
実に簡単ですね。教えるのが簡単＝直感的＝マスターするのも容易、という事です。
まだ論理的に考えることが難しい子どもにとって、分かりやすい事はとても大事です。

ですので、あくまでピコでは【１】の方法で習得を目指します。
また、都合上、ここでは【２】の解説は省略します。
わり算にはまだ“割り切れない問題”が残っているのですから。

さて、3級には四捨五入が登場します。
かけ算では指定通り、普通に四捨五入するだけ、と言えば話が早いのですが、わり算では割り切れずに仕方なく四捨五入する問題が一定数存在します。
例えば¥13÷0.094とか¥44÷0.263などですね。
上記の例では、ぱっと見た感じ、割り切れなそう、という事が分かりますか？？
まずは、この感覚を持ち合わせた方が有利です。
この２つは設問が明らかに不自然です^^;
出題者は割り切れないのを分かってほしい、とばかりに問題を作っていると思われます。

割り切れると思って割り切れない、のと割り切れないと思ってやっぱり割り切れないのではその問題に対する自信が大きく変わってきます。
なので、不自然な問題には不自然な問題なりに自信を持って対処？をしましょう。

あとは九九と引き算を間違えないことでほとんどが解決します。
これに関しては沢山問題をこなしていくことが合格への王道と言えるでしょう。

ここから先、お子様に伝えるのは各ご家庭の方針で決めてください。
受験で言う所謂“テクニック”に相当します。知っているか、知らないかですべてが決まる知識といったものです。

まずは割り切れないわり算の出題数です。
これは正直そこまで多くありません。と言うか予め問題数が決まっていたはずです^^;
（明言は避けますが…）
なので、全部が全部割り切れない何てことはなく、ほとんど割り切れてしまうのです。
よって、四捨五入ばかりしているというのはあり得ません。それを念頭に入れておけいこに励みましょう。

続いて桁数？の問題です。

3級では答えがながーーーく続くことはありません。
最長で4つの数字に収まります。例えばですが、111.111なんて事にはならないのです。
割り切れる場合も割り切れない場合も、もっと早く終了します。
あまりに計算が長く続く場合はこれは間違いだ、と早めに気付く事が必要です。
迷っている暇は無いのですから…

さて、3級を長々と解説してきましたが、特徴は把握できましたか？
単純な桁数の増加はほとんどなく、小数点や割り切れない、などの問題が課題になる3級です。

それでは最後に合格点。

掛け算　　　20問100点満点（1問5点）
割り算　　　20問100点満点（1問5点）
見取り算 10問100点満点（1問10点）

300点満点240点以上で3級合格です。

…。
……。

気付かれましたか？合格点の高さに。
うっかりミスを連発したらすぐに落っこちます。何事にも揺るがないメンタルも必要なのです。日商検定では特に。

小数点もついて、割り切れない問題も出て、合格点が1割上昇するという、抜け目ならない3級でした。沢山練習して揺るがない自信を身に付けていきましょう。

計算力・集中力・忍耐力・判断力、記憶力・想像力・発想力など、一生モノの力を身につけられます。そろばん脳(頭の中のそろばん)を作れます。

よろしければ、キャットリーの特長やそろばんの効果についてもご覧ください。

オンライン校もあります。教室での対面の授業と遜色ない授業をオンラインで実施します。ぜひ体験授業にご参加ください。